
Ankerがアクセサリーのように耳に付けるイヤーカフ型ワイヤレスイヤホン「Soundcore AeroClip」を販売開始
2025/04/23 11:00:44
[quads id=1]
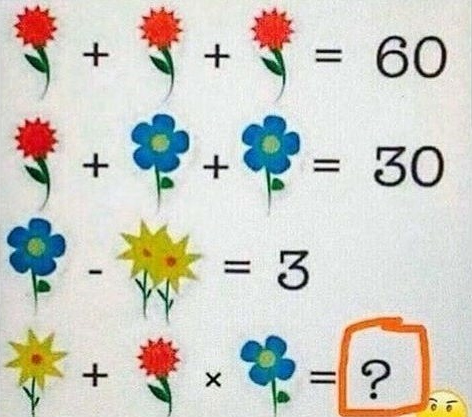
[quads id=2]
海外で話題になっている算数の問題がある。それは、3種類の花を使った3つの式から、それぞれの花が数字のいくつにあたるのか推測していくものだ。
1つ目の式は、赤い花が3つ足され、合計が60となっている。このことから、赤い花1輪は「20」ということが分かる。
2つ目の式は、赤い花と青い花を足す問題だ。式の答えは10。赤い花は20と分かっているので、青い花の数が導き出せる。青い花は「5」である。
3つ目の式は、先ほどの青い花から黄色い花を引く問題だ。青い花は「5」なので、黄色い花は1輪で「1」だと分かる。青い花「5」から黄色い花2輪を引き、答えは「3」となる。
そして肝心なのは最後の問題である。「黄色い花+赤い花×青い花=?」という問題だ。小学生のほとんどは正解するそうだが、大人は間違ってしまいやすいという。子どもの観察力の凄さがうかがえる。
実は、これに似たような問題が日本でも今年の2月に話題になった。リンゴ、バナナ、ココナッツを足して最後の答えを導き出すという問題で、答えの導き方は同じ。だが、やはり多くの人が間違っていた。このような問題は、どうやら計算能力よりも観察力が必要となってくるようだ。花の問題も答えることができるかな?
[quads id=4]
ゴゴ通をフォローする








2025/04/23 11:00:44

2025/04/18 01:03:00

2025/04/18 12:00:57

2025/03/15 12:45:29

2025/01/10 11:09:17

2024/12/19 11:56:14

2024/09/10 04:34:45

2024/08/29 08:21:33

2024/08/09 10:26:55

2024/07/23 09:38:23

2025/04/23 11:00:44

2025/04/18 01:03:00

2025/04/18 00:00:57

2025/04/11 00:00:33

2025/04/05 00:02:40

2025/04/04 22:35:21

2025/03/27 18:11:15

2025/03/15 00:45:29

2025/03/13 19:41:21

2025/03/12 23:18:59




まず、この記事を書いた人間は、
ちゃんと日本語の勉強をしよう
助詞の使い方がデタラメですね
いつの話だよこれ・・・
取り敢えず?の右下の顔アイコンなんやねん
青い花だけど5であることがわかるのは花弁が5枚のもの
最後の問題で出てきている花弁4枚のものは未定義
花弁の枚数がそのまま値を示すという定義は見受けられないので花弁4枚の青い花の値は未定義
なので1+20×?で回答不可能
そこまで言うなら、「何故黄色の花が2輪重なったアイコンは2だが、1輪のものは未定義」まで言わないのか
というか、カッコつけて「定義」とか使いたがるエセ理系がこういうところでバカな議論をしてくれちゃうと、理系としては迷惑
括弧付けてるのが返信者というギャグなのかな?
答えを81に限定したいなら
赤花は花びら20枚、黄花は花びら1枚にすべきだよな
定義に一貫性がないから無駄に混乱を招いてる
現状の問題だと101でも102でも解なしでも正解でもいいはず
(102の場合は単に色=数字という定義)
あと関係ないけど、定義は理系だけとは限らないよ
文系の論理学や心理学でも普通に使う
これって「赤い花」「青い花」「黄色い花」が代数を表してるのは分かるんだけど
計算するときに「花」じゃなくて「花の色」で考えるから
1つ目の式は赤+赤+赤=60で赤=20
2つ目の式は赤+青+青=30 一つ目の式を赤に代入して青=5
3つ目の式で黄色い花の項が1つなので青-黄=3 1つ目と2つ目の式をそれぞれ赤と青に代入して黄=2
(本当は青-2黄=3なので 1つ目と2つ目の式をそれぞれ赤と青に代入して黄=1)
最後の黄+赤×青=?で赤黄青それぞれに代入して2+20×5=102
って間違えるんだと思ったんだけど違うのかな?
答えどこ?
こういう類の問題って大概問題そのものが複数解釈が可能でその判断基準が書いてないってだけの代物なんだよねぇ。
回答者ではなく出題者が無能なだけな気がする。
大学の論証系のテストなら、答えはいくらでも出せそうだね。
中学とかなら柔軟な先生じゃない限りバツにされそうだけど。
答え101じゃないの?
で、答えは?
普通に代数で考えれば
答えは102。
1+20×10=2001?
みんな、よく見るんだ。
黄色い花: 3番目の式では2本、4番目の式では1本。
青い花: 2番目&3番目の式では花びら5枚、4番目の式では花びら4枚。